The triangular distribution is popular in risk analysis because it seems to naturally embody the idea of ‘three point estimation’, where subjective judgement is used to estimate a minimum, a ‘best guess’ and a maximum value of a variable such as the cost of an item or the time taken to accomplish a task. It looks mathematically simpler than many of the standard distributions and could be regarded as the simplest probability density function that embodies a random variable with a given minimum, mode and maximum. Because of this, you may be tempted to think of it as the distribution that involves fewest assumptions and that it is therefore the one to use when you don’t know what the real distribution is. Its Wikipedia article says ‘… the triangle distribution has been called a “lack of knowledge” distribution’. Although the article gives no reference for this assertion, and I’ve never seen it explicitly stated anywhere else, it sounds plausible and I do think it represents the main reason people use the triangular distribution.
The problem with this idea is that it isn’t true. The triangular distribution is absolutely NOT the maximally non-committal distribution consistent with these constraints. That distribution is the one with the biggest entropy, and it isn’t triangular. Before discussing this, however, it would be a good idea to mention a couple of other reasons why you shouldn’t use the triangular.
Firstly, its apparent simplicity is illusory. Generating triangularly distributed pseudo-random numbers is no faster than for many other distributions, though the relative speed varies depending on the distribution you are comparing it with and on the algorithms used. Comparing it with the normal distribution, and using the inverse transform method for both distributions, the triangular is slightly faster, but not by enough to justify choosing one over the other. Using other algorithms the normal tends to be faster.
For example, using GNU Octave and the inverse transform method, on my computer it took 4.9s to generate ten million samples from the triangular distribution whereas the same number from the normal distribution took 5.6s—a very small difference. Using Stein & Keblis’ ‘minimax’ method for the triangular and Octave’s built-in function normrnd, which uses Marsaglia and Tsang’s ‘Ziggurat’ method, again with a sample size of ten million, the triangular took 2.9s and the normal 1.5s. The ‘R’ programming language has a triangular random function in its ‘triangle’ package written and maintained by Rob Carnell. Using this and R’s built-in normal random function, also with a sample size of ten million, the triangular took 6.9s and the normal 5.1s.
The triangular distribution’s claimed ‘simplicity’ therefore confers little or no advantage in terms of computational speed.
Secondly, no random phenomenon commonly encountered in the real world actually has this distribution. Have you ever seen a set of real-world data distributed that way? No, of course you haven’t. That’s because, to the best of my knowledge, no real phenomenon is triangularly distributed, certainly not the cost of a widget or the time taken to accomplish a task in a project plan. The triangular is therefore the only distribution that you can be certain doesn’t apply! That should be a good enough reason by itself not to use it.
Finally we come to the question of how to find the real ‘lack of knowledge’ or maximally non-committal distribution. This is the one with the biggest entropy subject to the given constraints, which in the case of ‘three point estimation’ are specified values of a minimum, a maximum and a ‘best guess’.
The entropy of a probability distribution is a measure of its information content or, rather, its lack of it. That is, the lower the entropy, the more the distribution tells us about the variable it describes. It is defined by the following formulae:
For discrete distributions: $$\begin{equation} H = -\sum_{i} p(x_i) \ln p(x_i) \end{equation}$$ where \(i\) ranges over all values for which \(x_i\) is defined.
For continuous distributions: $$\begin{equation} H = -\int_{R} f_X(x) \ln f_X(x) dx \end{equation}$$ where \(f_X(x)\) is the probability density function and \(R\) is a portion of the real line that includes all values of \(x\) for which \(f_X(x) > 0 \), and could extend to infinity in one or both directions.
A discrete distribution that consists of one certain event has an entropy of zero. That is, zero entropy represents complete certainty or complete information. If we are less than completely certain about the outcome, then the entropy is positive. Continuous distributions can have negative entropies but it is still the case that lower entropy corresponds to more information.
The challenge is to find the function \(p(x)\) (in the discrete case) or \(f_X(x)\) (in the continuous case) for which \(H\) is a maximum subject to whatever constraints we wish it to have. This will give us the distribution whose only information content is the values of our constraints. That is, the true lack of knowledge distribution.
The mode of a probability distribution isn’t much use as constraint in a maximisation problem because all it tells us is that there exists a value of \(x\) that is more probable than any other value of \(x\). This doesn’t constrain the distribution very much. It could include, for example, a uniform distribution where one probability is larger than all the others, but only infinitesimally. This would, for all practical purposes, be indistinguishable from a true uniform distribution. For it to be any use as a constraint we would also need to specify something about the shape of the peak. In other words, the mode is useful as a parameter to characterise a distribution when its functional form is already known but not as a way of finding that functional form in the first place.
Fortunately, the mode is not the right way to characterise a ‘best guess’. Although a naive person may think that the ‘best guess’ should be the most likely outcome, in fact it should be the mean. Statisticians call the mean ‘expected’ because it is rational to act as if the mean is going to happen, even though it might not. For example, if you play a game of chance \(n\) times, then, if \(n\) is big enough, you will win \(n \times\) the mean of its distribution, not \(n \times\) the mode or \(n \times\) the median, unless these accidentally happen to coincide with the mean.
Furthermore, the mean of the sum of several random variables is equal to the sum of their means but, unless it coincides with the mean, the median is not the sum of the medians and the mode is not the sum of the modes. If, for example, you are building a widget out of numerous components, then you would want the ‘best guess’ of the cost of the widget to be the sum of the ‘best guesses’ of the costs of its components. This can only happen if you use the mean.
The maximum entropy distribution with a minimum, \(a\), mean, \(\mu\), and maximum, \(b\), is, in fact, a truncated exponential function given by:
$$ \begin{equation} f_X(x) = \begin{cases} \dfrac{\alpha e^{\alpha x }}{e^{\alpha b } – e^{\alpha a }} & a \leqslant x \leqslant b\\ 0 & \text{otherwise} \end{cases} \label{eq:trunc_exp_a_b_finite} \end{equation} $$
Where \(\alpha\) is a constant. Figure 1 below illustrates three examples of this distribution. They all have \(a = 1\) and \(b = 5\), but each has a different value of the constant \(\alpha\), which is fixed by the value of the (user chosen) mean \(\mu\). The curve on the left has \(\mu = 2.6\), the one in the middle has \(\mu = 3.0\) and the one on the right has \(\mu = 3.4\). These illustrate the fact that that if the mean is to the left of the halfway point, the curve slopes downwards, if it is to the right it slopes upwards and if it is exactly halfway between \(a\) and \(b\) the distribution is uniform.
Figure 1: Examples of the truncated exponential distribution.
You may find the shapes of these curves a bit surprising. However, statistics is full of counter-intuitive stuff, so you should expect to be surprised. To hopefully convince you they are correct, Figure 2 below shows an animation of a ‘genetic algorithm’ that calculates a discrete version with 100 points. Its parameters are the same as those in the right hand graph in Figure 1, i.e. \(a = 1\), \(b = 5\) and \(\mu = 3.4\).
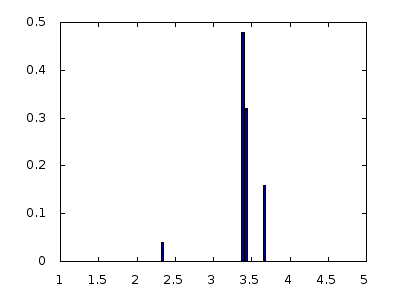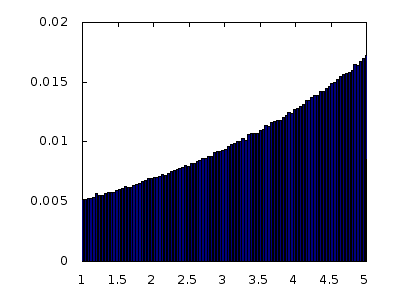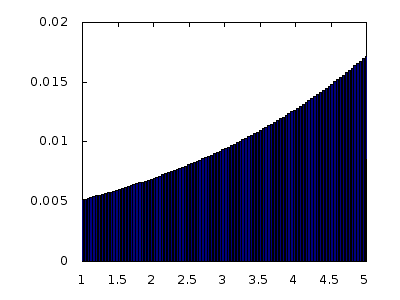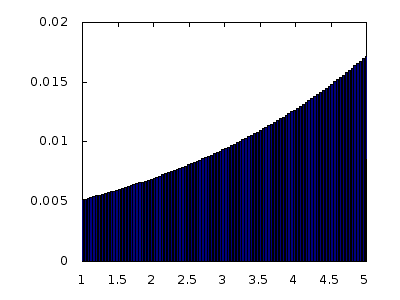
Figure 2: Evolution of a truncated exponential.
The first frame of the animation, i.e. the starting point of the algorithm, has just two bars, one each side of the mean. The distribution is then subjected to a series of mean-preserving random mutations that are accepted if the resulting distribution has a higher entropy but rejected if its entropy is the same or lower. Each step takes the distribution closer to the maximum entropy. It is plain to see that this looks exactly like the truncated exponential.
The vertical axis scale in Figure 2 is different from that in Figure 1 because it shows a discrete distribution while Figure 1 shows a continuous one. The sum of the bar heights in Figure 2 and the area under the curve in Figure 1 are both equal to unity.
The discrete maximum entropy distribution corresponding to a specified mode would be uniform, apart from the bar representing the mode, which would be taller than all the others, but only by an amount equal to the smallest number your computer is capable of storing. This suggests that if you really do prefer the mode instead of the mean as your ‘best guess’, you should actually choose a uniform distribution. That is, if you know with certainty that a variable is in a range \((a, \, b) \), then knowing that one value in that range is ‘most likely’ doesn’t increase your knowledge, unless you also know how much more likely it is, which would require an extra piece of information. Knowing the mean, on the other hand, does tell you something new about the variable’s behaviour.
I expect you are now wondering what the maximum entropy distribution is that corresponds to a specified median? Well, it’s a step function, with the step at \(x = median\). Figure 3 below shows three examples with the median at the same positions as the means in Figure 1.
Figure 3: Examples of the median step function distribution.
And here’s an animation identical to the previous one, except that is uses a median-preserving random mutation:

Figure 4: Evolution of a median step function distribution.
Both the truncated exponential and the median step function reduce to the uniform distribution when their middle parameter (the mean in the first case and the median in the second) falls mid way between the two end points. This is sensible because the uniform distribution has its mean and its median at its mid point, and has the highest entropy of all bounded distributions with the same end points. This suggests an additional criterion for a distribution to be suitable for ‘three point estimation’. It is that it should reduce to the uniform distribution whenever its ‘best guess’ parameter is located at its mid point. The triangular distribution fails this test, which is another reason not to use it.
The entropy of the truncated exponential isn’t always bigger than that of the triangular with the same end points, but it is always bigger than that of one with the same mean. The same applies to the median step function with respect to the median. The uniform, however, beats all triangular distributions between the same end points.
So, if you are certain that your random variable has hard upper and lower bounds, you can choose between the
- uniform,
- truncated exponential and
- median step function
distributions, in that order, but not the triangular. Of these, you should probably choose the uniform unless you have a good reason not to.
However, it isn’t always sensible to choose a distribution with hard upper and lower bounds. Real-world uncertain phenomena, particularly costs, sometimes surprise us by turning out wildly different, usually worse, than we expected, which can be embarrassing.
In risk analysis people tend to prefer bounded distributions because, they argue, all real-world phenomena are bounded. But it is often difficult to know exactly where the bounds should be, so it easy to get them wrong, and often there is no meaningful way of saying what they should be anyway. For example, if the height of the tallest human who has ever lived is \(h \, \textrm{cm}\) then can you really say that it is impossible for someone ever to grow as tall as \((h + 1)\textrm{cm}\)? If not, should you take \((h + 1)\) as the upper bound? And if not that, should it be \((h + 2)\) and so on ad-infinitum?
Many real phenomena actually do conform to unbounded distributions, with apparent boundedness resulting from the low probability of values far from the mean rather than an actual hard upper or lower bound. For example, although the normal distribution extends to infinity in both directions, its probability density becomes very small very fast as you move away from the mean in either direction. The probability of a normal random variable turning out greater than six standard deviations from the mean is smaller than the probability of winning the EuroMillions jackpot. This means that using it in a risk simulation almost certainly won’t produce a value that far from the mean unless you use \(10^{10}\) or more iterations. In fact, the real problem with the normal is that it tails off too fast and in many cases actually underestimates the risk of values far from the mean.
Fortunately, the maximum entropy method can easily handle unbounded situations. A useful one for risk analysis is obtained by maximising the entropy subject to the constraints that \(X\) has a specified lower bound \(x_0\) and mean \(\mu\), but no upper bound. This turns out to be the exponential distribution:
$$\begin{equation} f_X(x) = \begin{cases} \lambda e^{-\lambda (x – x_0)} & x \geqslant 0 \\ 0 & \textrm{otherwise} \end{cases} \end{equation}$$
This turns ‘three point estimation’ into ‘two point estimation’. If \(x_0 = 0\) it can be used for variables that cannot be negative, which is often the case with the costs of things, though not always, as sometimes someone might pay you to take an item off their hands.
There are lots of other maximum entropy distributions that you can use corresponding to various constraints, but it would be deviating too much from the purpose of this article to go into these, as well as making it massively longer, so this is probably a good place to stop.
So, in conclusion, after all this you may be wondering exactly what the triangular distribution is useful for. So am I.
If you have been, thanks for reading!
© Copyright 2016 Howard J. Rudd all rights reserved.